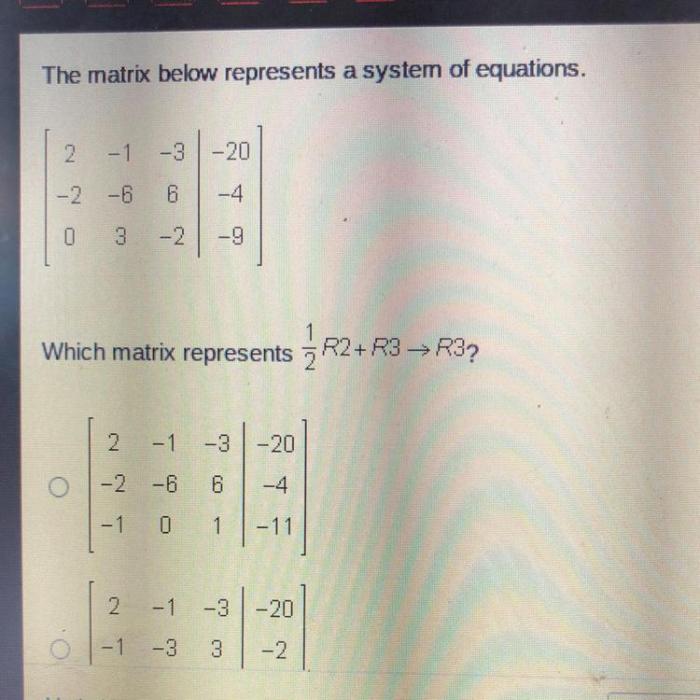
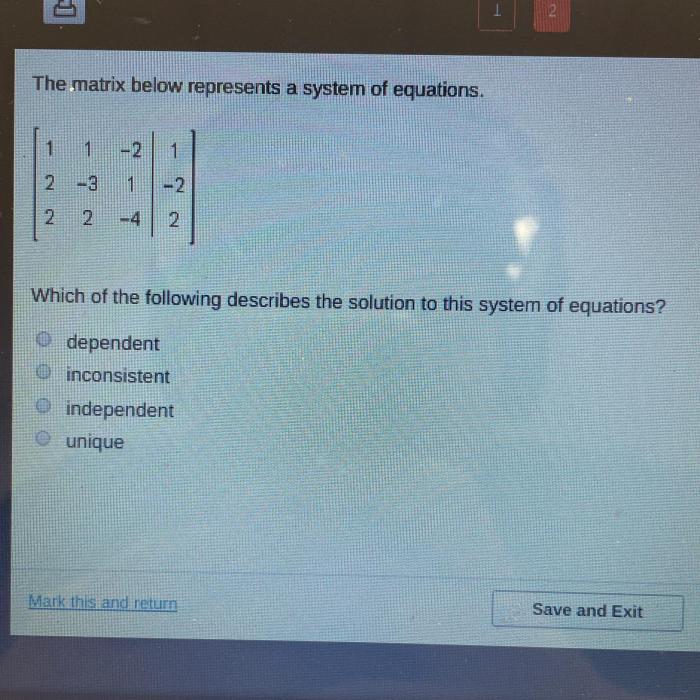
The matrix below represents a system of equations. – The matrix below represents a system of equations, an indispensable tool in mathematics and beyond. This intricate framework allows us to represent and solve complex systems of equations, unlocking a world of applications in diverse fields.
By harnessing the power of matrices, we gain a deeper understanding of the relationships between variables and equations, enabling us to tackle real-world problems with greater precision and efficiency.
System of Equations
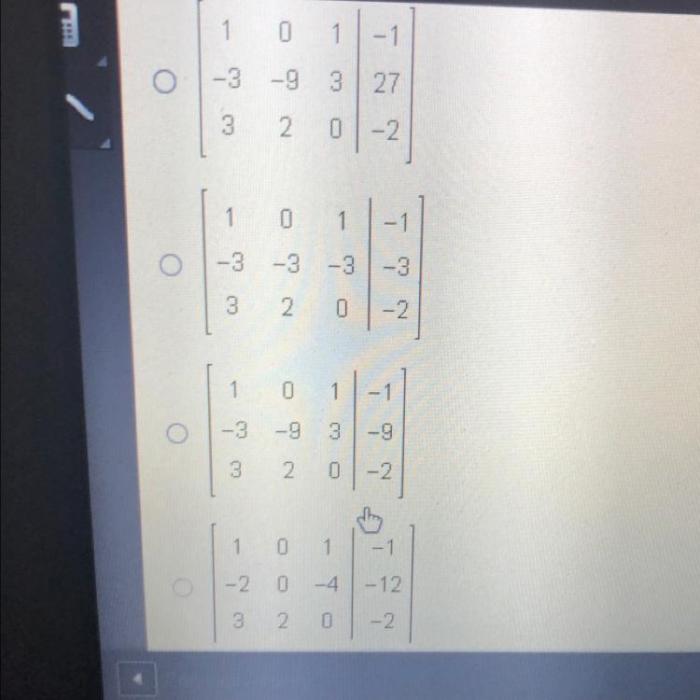
A system of equations is a set of two or more equations that share the same variables. The goal is to find the values of the variables that satisfy all the equations simultaneously.
Systems of equations can be represented in various forms, including:
- Two variables: y = mx + b, y = kx + c
- Three variables: 2x + 3y – z = 5, x – y + 2z = 4, 3x + 2y – 3z = 1
- Four variables: w + x – y + z = 0, x + y + z – w = 1, w – x + y + z = 2, x – y + z + w = 3
Matrix Representation: The Matrix Below Represents A System Of Equations.
A system of equations can be represented as a matrix. A matrix is a rectangular array of numbers arranged in rows and columns. The matrix representation of a system of equations is:
| Coefficient Matrix | Variable Matrix | Constant Matrix |
|---|---|---|
| [a11 a12 … a1n] | [x1] | [b1] |
| [a21 a22 … a2n] | [x2] | [b2] |
| … | … | … |
| [am1 am2 … amn] | [xn] | [bn] |
where a ijrepresents the coefficient of x jin the i thequation, b irepresents the constant term in the i thequation, and x jrepresents the j thvariable.
Solving Systems of Equations, The matrix below represents a system of equations.
There are several methods for solving systems of equations, including:
- Substitution: Solving for one variable in terms of the others and substituting it into the other equations.
- Elimination: Adding or subtracting equations to eliminate variables.
- Matrix Inversion: Using matrix operations to find the values of the variables.
Applications of Matrix Representation

Matrix representation of systems of equations has numerous applications in real-world problems, such as:
- Physics: Solving systems of equations to determine the motion of objects, forces, and energy.
- Engineering: Analyzing structural stability, designing circuits, and optimizing processes.
- Economics: Modeling supply and demand, forecasting economic trends, and managing portfolios.
FAQs
What is the relationship between a matrix and a system of equations?
A matrix is a rectangular array of numbers that can represent a system of equations. Each row of the matrix corresponds to an equation, and each column corresponds to a variable. The elements of the matrix represent the coefficients of the variables in the equations.
How can I solve a system of equations using a matrix?
There are several methods for solving a system of equations using a matrix, including substitution, elimination, and matrix inversion. Each method has its own advantages and disadvantages, depending on the size and complexity of the system of equations.